Uvodna sekcija (tematski format)

  • Opšta sekcija

  • Tema 1- Uvod u teoriju igara

    Osnovni cilja ovog predavanja su da objasni:

        1.       Šta je „teorija igara“?
    2.       U kojim naukama se koristi teorija igara?
    3.       Gde se koristi u svakodnevnom životu?
    4.       Ko je bio Džon Neš?
    5.       U teoriji igara, šta podrazumevamo pod agentom?
    6.       U teoriji igara šta podrazumevamo pod isplatom?
    7.       Na koji način se određuje vrednost isplata u teoriji igara?
    8.       U kojim se nauka koristi teorija igara?
    9.       Šta se podrazumeva pod terminom „igra“?
    10.   Koju strategiju će odabrati agent?



  • Tema 2 - Teorija igara u širem smislu

    Osnovni cilj ovog predavanja su da objasni:

    1.   1. Kakve vrste igara postoje u zavisnosti od interesa igrača?
    2. . Kakve vrste igara postoje u zavisnosti od elementa slučajnosti?
    3.   Kakve vrste igara postoje u zavisnosti od broja igrača?
    4.    Kakve vrste igara postoje u zavisnosti od broja mogućih strategija?
    5.  . Kakve vrste igara postoje u zavisnosti od opsega informacija koje poseduju igrači?
    6.    Šta se podrazumeva pod pretpostavkom da su igrači savršeno racionalni?
    7.    Šta je Nešov ekvilibrijum?
    8.    Ukoliko promenom svog poteza jedan od igrača može da dođe u bolju (ostvari veću korist) poziciju da li je ta situacija Nešov ekvilibrijum’
    9.     U situaciji Nešovog ekvilibrijuma da li su oba igraća postigla svoju maksimalnu dobt?

    1010. U situaciji Nešovog ekvilibrijuma da li je simultanom promenom strategija moguće doći do rešenja koje je korisnije za obe strane?

  • Tema 3 - Koncept najboljeg odgovora i Nešova ravnoteža

    1.   1.   Kakva je igra zatvorenikova dilema?
    2.       Da li je zatvorenikova dilemma kooperativna ili nekooperativna igra?
    3.      Da li sun a kraju igre učesnici u zatvorenikovoj dilemi dobili optimalno rešenje i zašto?
    4.      Šta znači dominantna strategija?
    5.      Kakva sve dominantna strategija može biti?
    6.     Šta su kooperativne igre?
    7.     Šta su nekooperativne igre?
    8.     Kako rešiti igru pomoću mehanizma najboljeg odgovora?
    9.     Da li svaka matrica (igra) mora da ima nešovu ravnotežu?
    10.Da li matrica (igra) može da ima više ekvilibrijuma?

    Osnovni cilj predavanja su da objasni:




  • Tema 4 - Mešovite strategije i Nešova ravnoteža


    Osnovni cilj ovog predavanja su da objasni:

    1.        Šta su „mešovite strategije“?
    2.     Šta su „čiste“ strategije?
    3.     Šta su igre koordinacije?
    4.     Šta su igre čiste koordinacije?
    5.       Šta je fokalna tačka?
    6.       Kakva verovatnoća karakteriše čiste strategije?
    7.      Kakva verovatnoća karakteriše mešovite strategije?
    8.      Kako se utvrđuje ravnoteža igra koja nema Nešovu ravnotežu?
    9.     Kako objašnjavamo korisnost igrača u mešovitim strategijama?
    10.     Da li postoji više ravnotežnih ishoda u igrama koordinacije?



  • Tema 5 - Koncept alternativnog rešenja

    Osnovni cilj ovog predavanja su da objasni:
    1.     Kako funkcioniše metoda isključenja dominantne strategije?
    2.     Na koji način igrači mogu jednostavnije da odlučuju i donose strategije?
    3.     Šta su minmax strategije?
    4.   . Kako funkcioniše metoda sukcesivne eliminacije suvišnih strategija?
    5.     Da li metodom dominacije možemo rešiti svaku strategiju?
    6.     Šta je ravnotežni par strategija?
    7.     Šta su podređene strategije?
    8.     Pod kojim uslovima se može eliminisati određena strategija?
    9.     Da li eliminacijom striktno podređenih strategija se može doći do Nešovog ekvilibrijuma?
    10. Zbog čeka se ponekad ne može utvrditi koja strategija je striktno podređena?



  • Tema 6 - Ekstenzivna forma igara

    Osnovni cilj ovog predavanja su da objasni:    

    1.       Koji načini prikazivanja igara postoje?
    2.       Šta su čvorovi odlučivanja?
    3.       Šta je početni čvor?
    4.       Šta je terminalni čvor?
    5.       Šta su neterminalni čborovi
    6.       Kome pripadaju neterminalni čvorovi?
    7.       Da li svaka igra može da se prikaže u ekstenzivnoj formi?
    8.       U kakvom su odnosu potezi igrača?
    9.       Šta je strategija?
    10.      Šta je potez?





  • Tema 7 - Bajesove igre

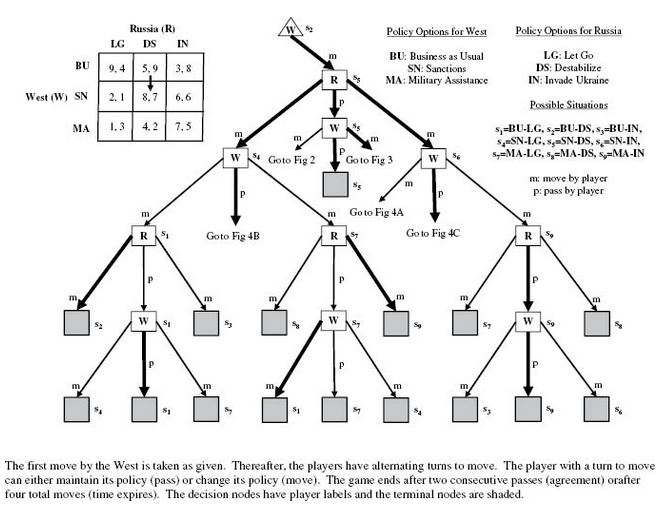
    Osnovni cilj ovog predavanja su da objasni:

    1.    

    1. Na koji način roba na aukcijama formira cenu?
    2. Šta je neivesno agentima u nemim aukcijama?
    3. Koja 4 elementa određuju Bajesove igre?
    4. Šta je Bajesov-nešov ekvilibrijum ?
    5. Šta je savršeni Bajesov ekvilibrijum?
    6. U signalizacionoj igri sa čime je upoznat „agent“?
    7. U signalizacionoj igri sa čime je upoznat „učesnik“?
    8. Koje uslove je neophodno zadovoljiti da bi igra imala perfektni Bajesov ekvilibrijum?
    9. Koja očekivanja treba da ispuni igra da bi to bio Bajesov-nešov ekvilibrijum?
    10. Hronološki, kojim redom povlače poteze igrači u Bajesovom ekvilibrijumu?



    1. Tema 8 - KOLOKVIJUM

      Poštovane kolege, ove nedelje nećete raditi novu lekciju već kao što je u planu i programu ćete imati kolokviijum. Kolokvijum obuhvata svo gradivo koje smo učili do sada. Kolokvijum će sadržati zadatke kao i teoretska pitanja. Na forumima pogledajte zadatke različite težine i pokušajte da ih uradite.





    2. Prebacivanje normalne u ekstenzivnu formu i obrnuto

      1. Da li se svaka ekstenzivna strategija može predstaviti kao normalna strategija?
      2. Da li se svaka normalna strategija bez obzira na broj učesnika može predstaviti kao ekstenzivna strategija?
      3. Da li je pri  prebacivanju iz ekstenzivne u normalnu formu važno koji igrač igra prvi?
      4. Da li je teže prebaciti strategiju iz normalne u ekstenzivnu formu?
      5. Da li se svaka normalna strategija formata 2x2 može predstaviti kao ekstenzivna strategija?

    3. Izračunavanje očekivane isplate

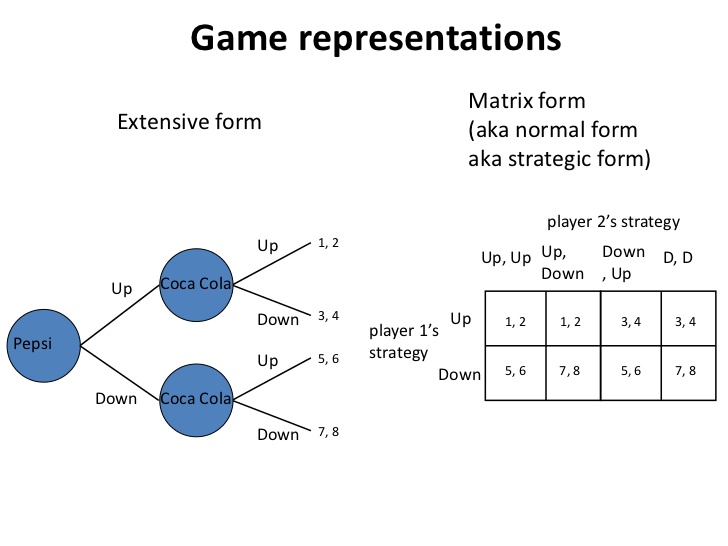
      U ovoj lekciji bavicemo se sledecim pitanjima:

      1. Da li je korisnost igrača I način zapisivanja ordinalna ili normativna?
      2. Da li u svakoj igri igrač dobija najveću isplatu?
      3. Da li je moguće da zbog nekoordinacije oba igrača završe u suboptimalnom ishodu?
      4. Da li je moguće da zbog nekoordinacije oba igrača završe u najboljem mogućem ishodu?
      5. Da li igra bitka polova predstavlja igru gde oba igrača mogu da zavše u najboljem mogućem ishodu?

    4. Tržišne strukture i primena teorije igara

      Pitanja za razmisljanje

      1. Koliko članova oligopola postoji u duopolu?
      2. Sta je bertranov model duopola?
      3. Na koji način je predstavljena matrica iplata u bertranovom modelu duopola?
      4. Šta oligopolista dobija ukoliko nastupa strateški kooperativno?
      5. Koji su oblici udruživanja zastupljeni kao vid kooperativnog nastupa oligopolista?




    5. Dinamničke ili sekvencijalne igre

      Pitanja za razmišljanje:
      1. Šta su dinamičke ili sekvencijalne igre?
      2. Koji igrač je lider?
      3. Koji igrač je satelit?
      4. Ukoliko ima više Nešovih igara da li se u slučaju dinamičkih igara može utvrditi koja je verovatnija?
      5. Da li ove igre mogu da se predstave u ekstenzivnoj formi?


    6. Igre sa zbirom nula (sa konstantnim zbirom)

      Pitanja i odgovori
      1.šta predstavljaju igre sa zbirom nula?
      2. Kakva je korisnost igrača u igrama sa zbirom nula?
      3. Kakva je islata igrača u slučaju igre sa zbirom nula?
      4. Da li su ovo kooperativne ili nekooperativne strategije?
      5. Da li rezultat može da bude Pareto optimalan?


    7. Minimax algoritam

      Pitanja za razmišljanje
      1.       O čemu se radi u minimax teoremi?
      2.       Cilj minimax ideje je?
      3.       Minimax je pravilo koje se odnosi na?
      4.       U kakvim igrama se koristi ova teorema?
      5.       Šta objašnjava makmin teorema?



    8. KOLOKVIJUM

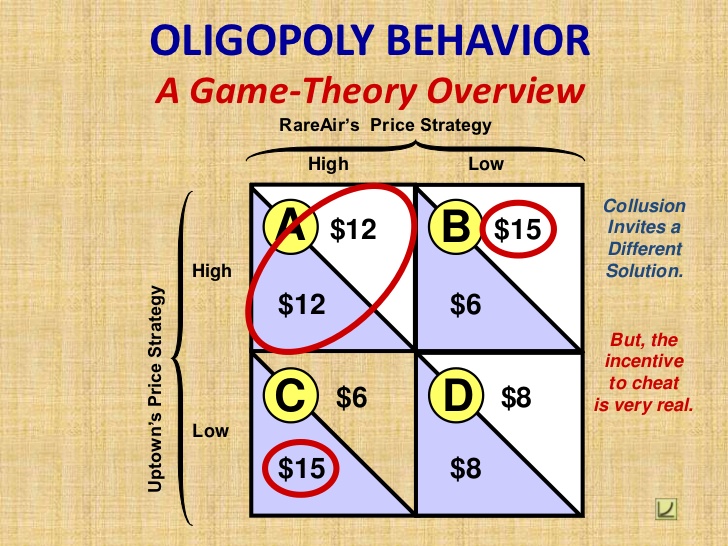
      Poštovane kolege, ove nedelje nećete raditi novu lekciju već kao što je u planu i programu ćete imati drugi kolokviijum. Kolokvijum obuhvata svo gradivo koje ste učili od osme lekcije do sada. Kolokvijum će sadržati samo teoretska pitanja.